微分、积分和微分方程4.1. 知识要点和背景:微积分学基本定理 4.2 实验与观察(Ⅰ):数值微积分4.2.1实验:积分定义、微分
2008-10-17 00:32

微分代数方程是一类微分方程,其中一个或多个因变量导数未出现在方程中。
2023-07-19 11:15
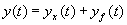
2-2 系统微分方程的解——系统的全响应 一、 线性系统微分方程线性的证明 线性系统必须同时满足齐次性与叠加性。所以,要证明
2009-07-09 09:45
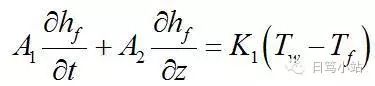
这一次日笃小编来教大家如何在simulnk里面,求解偏微分方程(Partial Differential Equation-PDE)。
2023-06-25 16:03
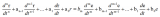
一、什么是微分算子符号? 描述线性系统的激励函数和响应函数间关系的微分方程,具有以下形式: 式中 为时域中的微分算子符号,当它们作用于某
2021-05-20 15:06
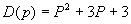
是: 其次,将介绍:系统相当于一个微分方程;系统相当于一个传输算子H(p);系统相当于一个信号——冲激响应h(t)。对系统进行
2009-07-09 09:39
Hinton创建的向量学院的研究者提出了一类新的神经网络模型,神经常微分方程(Neural ODE),将神经网络与常微分方程结合在一起,用ODE来做预测。
2018-06-26 11:19
研究人员已经开始探索使用ML在高性能计算方面提供持续改进的可能,以解决偏微分方程和科学计算中的困难计算问题。
2019-07-30 10:20
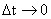
根据牛顿定律,运动物体总是有趋于静止,或保持运动的特性,我们把物体所具有的这种状态,叫做稳态,与此相反的非稳态,叫做瞬态,瞬态是反应物体变化过程的模型。
2023-02-07 10:36
TensorFlow 不仅仅可以用于机器学习。在此教程中,我们所举的例子(较为寻常)是使用 TensorFlow 模拟偏微分方程的行为(https://en.wikipedia.org/wiki/Partial_differential_equation)。我们将模拟几个雨滴落在方形池塘水面的情形。
2018-12-06 14:07