为提高超椭圆曲线上标量乘计算效率,将椭圆曲线上的斜-Frobenius映射推广到超椭圆
2018-02-05 15:35
在分析椭圆曲线密码体制的基础上,利用椭圆曲线离散对数问题的难解性,设计了一个新的基于椭圆
2010-02-26 15:52
椭圆曲线上的点构成的代数系统可以为密码学提供多种应用方案,本文基于椭圆曲线的数字签名方案给出了一个秘密共享方案,并对该方案的安全性进行了分析。该方案的安全性建
2009-06-19 08:22
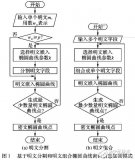
针对存储椭圆曲线密码加密生成的密文与明文相比需要的存储空间较多的问题,提出了一种基于明文长度的构建椭圆曲线密码密文的方法。首先,该方法通过分析
2018-01-02 17:19
近年来,通信领域得到了巨大的发展,网上银行、移动通信等应用増加了资源受限环境下的安全需求。与传统密码算法相比,椭圆曲线密码体制( Elliptic curve cryptography,ECC)提供
2021-05-13 11:43
椭圆曲线密码体制的快速实现依赖于标量乘(nP)的有效计算,该文改进的二进制和三进制的混合表示方法,并且将其推广到的二进制、三进制和五进制的混合表示。该算法在已知二倍
2009-04-16 09:57
提出了两个基于椭圆曲线的多重盲签名方案,该方案可以同时完成盲签名和多重签名的任务而且签名尺寸不会随签名人数增加而增加。还对方案的正确性、盲性、不可伪造性作了
2009-06-09 11:22
提出了一种基于椭圆曲线密码体制(ECC)的Schnorr型(t,n)门限数字签名方案,并对该方案的安全性进行了分析。方案由系统初始化、子密钥产生过程、签名过程和签名验证
2009-09-25 15:39
分析当前密钥协商方案, 讨论其安全性和攻击行为, 并对GDH 的安全性能和运算复杂度进行分析, 根据安全性需要, 给出了一种基于椭圆曲线的群密钥协商方案, 该方案不仅提高实
2010-01-15 15:34
基于椭圆曲线离散对数困难问题,结合KEM-DEM混合加密结构,提出一个新的无证书混合加密方案。采用椭圆曲线签名算法保证用户自主生成公钥的不可伪造性,利用用户公钥生成的会
2009-04-11 09:21