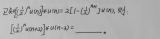
的卷积,需要熟练掌握其计算方法,并且要记住结果。为了方便大家对比,帮助理解和记忆,我把连续时间信号的卷积积分与离散时间信号的卷积和放在同一张表格中。 (二)
2021-09-29 17:28

考虑到许多读者可能对Poly并不了解,而且许多Poly文献读起来也比较抽象,我们先简单介绍一下Poly的工作原理。我们力图用最简单的代数与几何描述来解释Poly的基本原理。这部分内容参考了文献[12]的图片,我们通过解读这些图片来解释其中原理。
2023-07-17 14:19
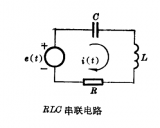
分析线性系统的古典方法是微分方程法。描述系统的微分方程中,包含有激励函数和响应函数以及它们对时间的各阶导数的线性组合。线性系统的分析归结为求解线性微分方程。因为这样一个分析求解的过程,都是在时域中进行的,所涉及的都是时间变量t,所以这种解微分方程的方法称为时域分析法。 进行时域分析时,首先是列出系统的微分方程,这个工作并不困难。对于线性电路,只要根据基尔霍夫定理,就可以列出一个或一组电路的线性微分方程
2021-05-20 13:59
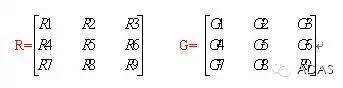
那可是天文数字,而且这里面绝大部分的矩形有重叠,重叠意味着什么?在算求和的时候有重复性的工作,其实我们是可以有效的利用已经计算过的信息的。
2019-08-09 16:09
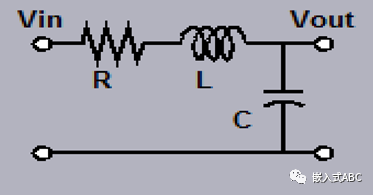
线性非时变系统定义给我们带来了许多数学工具,也包含卷积积分,傅里叶变换和拉普拉斯变换。
2023-10-17 10:31
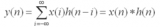
取反使得h(i)以纵轴为中心翻转180度,所以这种相乘后求和的计算法称为卷积和,简称卷积。 另外,n是使h(-i)位移的量,不同的n对应不同的卷积结果。如果卷积的变量是
2017-11-28 17:54
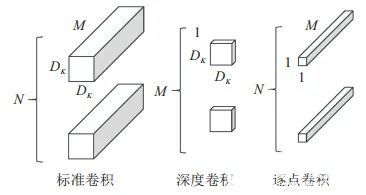
为MobileNet, 通过将标准卷积分解为深度卷积和逐点卷积, 保留多尺度预测部分, 以有效减少参数量. 对于检测得到的边框信息, 利用Deep-SORT算法进行跟踪. 实验结果表明, 所提出方法在跟踪效果基本不变
2022-11-09 10:23
的数学变换。 它能够揭示信号的频率成分,是信号处理中的基础工具。 卷积 : 是一种积分运算,常用于信号处理中,表示一个信号对另一个信号的响应。 在数学上,卷积是通过一种特定的积
2024-11-14 09:33
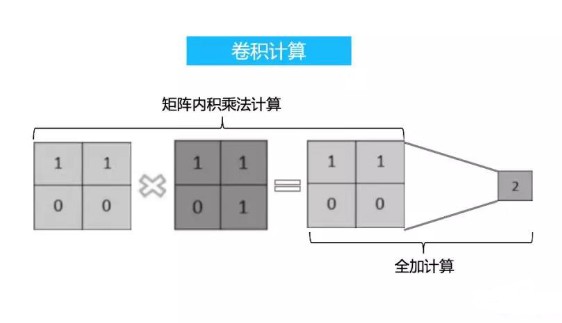
卷积过程是卷积神经网络最主要的特征。然而卷积过程有比较多的细节,初学者常会有比较多的问题,这篇文章对卷积过程进行比较详细的解释。
2019-05-02 15:39

疑问,主要原因来自于卷积计算“图解法”所带来的误导。图解方法只能帮助确定卷积的阶段和积分上下限,求解卷积结果还是需要根据实际信号函数进行计算。01 三角波
2023-12-18 16:19