提到蒙特卡罗(也有翻译成“蒙特卡洛”)一词,人们不禁想到摩纳哥的赌城。这两者之间有必然联系么?答案是:Exactly!下面就随网络通信小编一起来了解一下相关内容吧。 大家想想,赌博跟什么有关?首先想到的是随机性和概率性。对,那蒙特卡罗方法就是与概率论
2018-05-10 10:30
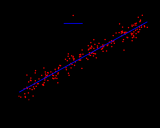
这两种方法的目标不同,尽管使用的方法类似。机器学习算法的评估使用测试集来验证其准确性。统计模型可以使用置信区间,显着性检验和其他检验对回归参数进行分析,以评估模型的合法
2019-04-08 08:55
这条公理表示为如果两事件互斥(即两事件不可能同时发生),那么这两个事件其中有一个发生的概率等于各个事件发生的(边缘)概率之和。我早说过了,这让人疑惑。让我们尝试通过第一篇中的一个例子来说明。
2018-09-24 09:31
傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。
2023-01-12 11:17
有人说,概率论线性代数要预先精通;有人说,微积分要懂一点;也有人说,没必要特地去补;甚至有人专门写了绕开数学的深度学习入门教材。
2018-08-20 14:24

但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一
2019-06-29 09:34

但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一
2023-07-17 10:18
本文主要介绍了什么是人工智能、对人工智能的科学进行了详解,其次介绍了学人工智能需要哪些知识,最后详解说明了从零开始学人工智能方法介绍。
2018-01-10 09:38
本文介绍了什么是人工智能、人工智能的研究价值、为什么人工智能突然变热的原因、其次分析了人工智能的社会价值、人工智能应用领
2018-01-10 14:26

二项分布的推导过程主要基于组合数学和概率论的基本原理。假设有一个随机试验,每次试验只有两种可能的结果,通常称为“成功”和“失败”。
2024-03-13 09:47